Modern zero-knowledge applications involve increasingly large and complex relations, that push the boundaries of memory constraints on consumer-grade machines. Proof composition allows us to reduce prover space complexity and proof size by embedding arbitrarily complicated subprotocols inside the main statement. Standardised “outer protocols” can also function as an “API” allowing for interoperability between proof systems.
A variety of composition strategies have emerged for constructing “hybrid” proof systems that combine components across the stack. The following taxonomy serves as a starting point for classifying representative examples of these strategies; it is not meant to be a final or comprehensive overview.
Recursive verification
Recursive verification reduces prover space complexity by breaking down a large statement into smaller subprotocols, which can be proven in parallel and then composed using proof-carrying data. Expensive computations such as non-native field arithmetic or bitwise operations can also be performed in embedded sub-protocols, which are cheaper to verify in-circuit than to prove.
(Image taken from https://twitter.com/recmo/status/1580627865594314752/photo/1)
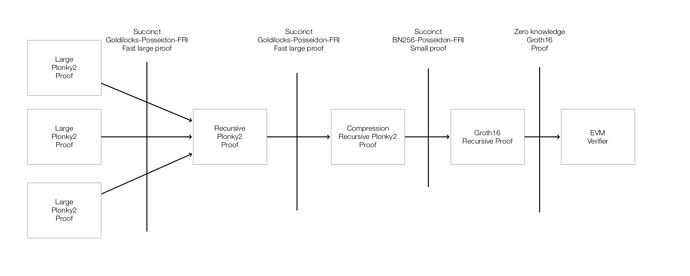
Recursive verification can also be used to compose “inner” and “outer” proof systems, allowing for the navigation of the prover/verifier complexity tradeoff. For instance, Polygon Hermez’s zkEVM uses the STARK proof system as an “inner” prover, taking advantage of its fast proving time to efficiently process a complex EVM state transition. However, this produces a large proof, which is expensive to verify on the resource-constrained blockchain execution environment. To shrink the proof size, a STARK verifier is implemented in a Groth16 “outer” prover, producing a constant-sized proof attesting to the validity of the inner STARK proof.
By composing fast-prover “inner” proofs with fast-verifier “outer” proofs, we achieve both prover space-efficiency and verifier time-efficiency. This highlights an interesting optimisation vector: to design better “inner” proofs, whose verifiers can be obfuscated with high efficiency, but whose provers can be large.
Another example, from a recent work by Consensys R&D [BSB22], presents a generic technique for efficiently recursing the GKR protocol inside another SNARK. GKR is a public-coin single-round interactive protocol: handling its randomnesses efficiently inside the non-interactive protocol involves replacing the Fiat-Shamir transform with a more efficient protocol.
Standardised functional commitments
Certain functional commitments are expressive enough to be considered as general APIs for inner proof systems. Different proof systems can be rephrased in the common language of functional commitments. These are of theoretical interest, since they reveal deeper similarities in structure, and possibly simplify security analysis. They can also be of practical interest, enabling efficient and interoperable constructions.
For instance, MPC-in-the-head can be thought of as a standard API to integrate set membership proofs with other NP relations [GGAK21]. This is because the MPC protocol being used can easily operate over any domain, with no need to “match” the set membership approach and the NP relation.
The inner product argument [BCCGP16] can also be thought of as a way to “compile” a commitment to a private polynomial, into a commitment to a public polynomial consisting of random challenges from the IPA rounds.
A final example is the sumcheck argument [BCS21], which allows split-and-fold strategies to be expressed in terms of the sumcheck protocol. The sumcheck protocol simplifies security analysis because it satisfies strong soundness properties that facilitate arguing the security of the Fiat–Shamir transformation in the plain model [CCHLRR18].
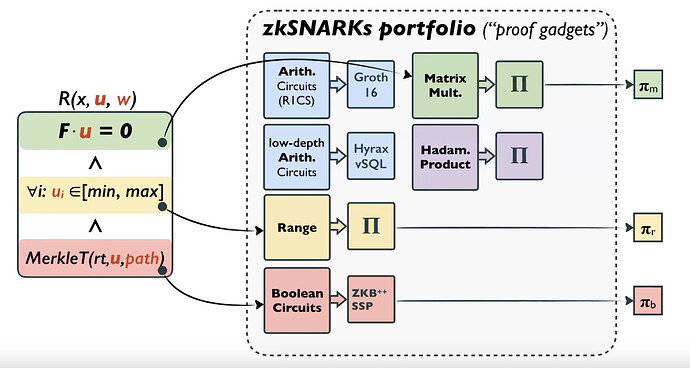
Linkable commit-and-prove SNARKs
LegoSNARK [CFQ19] augments specialised protocols with a generic “commit-and-prove” API, allowing for a statement proven using one protocol to be linked to other ones, using possibly different argument systems. Specialised protocols exploit the structure of their specific class of problem. For computations involving heterogeneous subroutines (e.g. arithmetic vs boolean), linking specialised arguments may be more efficient than trying to unify them in a single generic proof system.
The LegoSNARK authors introduce a generic gadget \textsf{CP_link}, which can be used to prove that two different Pedersen-like commitments open to the same vector. This is then used to compose gadgets for Hadamard products, linear relations, matrix multiplication, and more.
Statements can be broken down into structured problem classes and proven in special-purpose SNARKs. These small proofs can then be linked. [Image taken from: LegoSNARK Modular Design and Composition of Succinct Zero Knowledge Proofs - Dario Fiore (2019)]
This is similar in spirit to the proof of equivalence protocol for multiple polynomial commitment schemes, recently suggested in the context of Ethereum’s proto-Danksharding.